物理-数据双驱动求解非稳态流体运动,攻克神经网络对极坐标系兼容问题
近日,华东师范大学河口海岸全国重点实验室葛建忠研究员团队在采用融合物理信息的神经网络(PINN)求解非稳态流体运动方面取得突破。研究主要针对极坐标系下的浅水方程,建立了结合控制方程与稀疏数据的机器学习模型,实现了对方程的高精度求解。该方法重点解决了机器学习模型应用于极坐标系中可能出现的边界不连续问题,为PINN模型的发展与应用提供了重要启示。相关成果近日以Modeling Non‐Stationary Wind‐Induced Fluid Motions With Physics‐Informed Neural Networks for the Shallow Water Equations in a Polar Coordinate System为题发表于地球科学国际权威期刊Water Resources Research。
1 研究背景
近年来,人工智能技术迅猛发展,其在地球科学研究领域的重要性也日益凸显。尽管数据驱动的深度学习已展现出强大的能力,但数据匮乏问题在海洋研究中依然不可忽视。在此背景下,发展低数据依赖的人工智能方法显得尤为必要。
物理信息神经网络(Physics-Informed Neural Network, PINN)便是一类基于物理控制方程求解动力学问题的神经网络。然而,当前PINN的发展与应用仍面临诸多挑战,包括训练难度较高、难以处理复杂边界条件,以及对极坐标系的兼容性不足等问题,导致PINN目前更多地被应用于求解定常问题或其它相对简单的方程。
2 研究成果
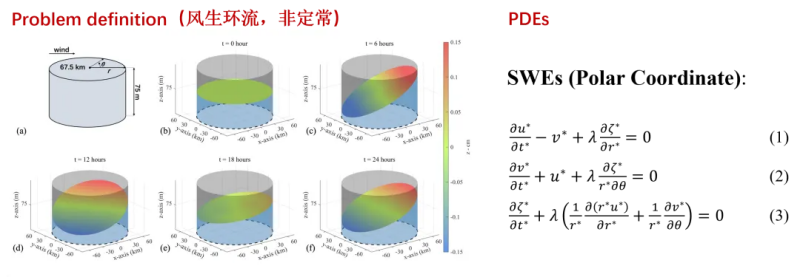
风生环流是一个经典的流体力学问题(图1),也常被用于数值模型的验证。这一流体运动过程可以用二维浅水方程加以描述,其解析解形式是定常运动与非定常重力波的叠加。对于神经网络模型而言,表达上述形式的解较为困难,因此采用融合稀疏数据的方式降低训练难度。
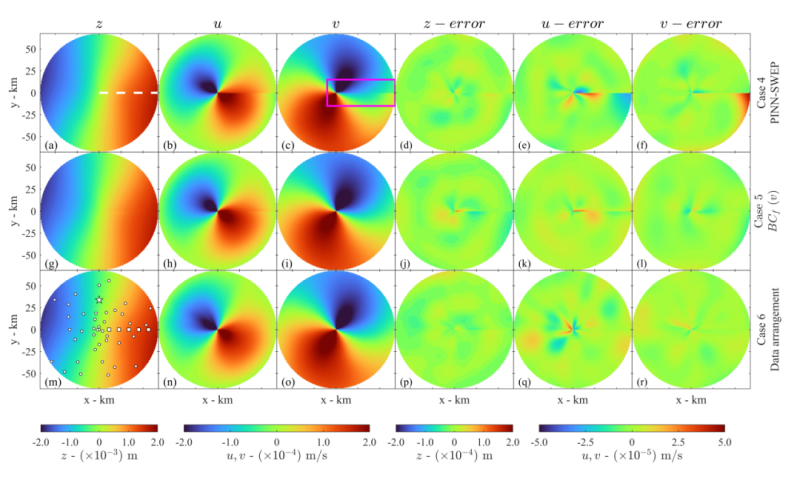
本研究所提出的PINN-SWEP模型,对上述问题实现了高精度求解。由于使用极坐标系时一般定义,或对于神经网络模型来说是两个“边界”,而真实物理问题中并不存在这两个边界,也并没有相应的“边界条件”来约束模型。导致常规的PINN模型在或时存在明显的不连续(图2),这对于神经网络在极坐标系下的应用是普遍存在的问题。针对这个问题,提出了“虚拟边界”(fictitious boundary condition, )的方法,即在损失函数中添加软约束,从而实现在不额外增加数据的前提下显著缓解边界不连续问题。该方法具有一定普适性,能够推动PINN在极坐标系下的应用。
图2. PINN-SWEP模型对水位与流速分量的求解结果;在采用了虚拟边界方法后,边界不连续问题得到显著改善
3 研究团队及资助
华东师范大学河口海岸全国重点实验室周在扬博士后为第一作者,葛建忠研究员为通讯作者,合作者还包括代尔夫特理工大学蒯宇博士、D.S. van Maren教授、Zheng Bing Wang教授等。研究得到国家重点研发计划(2022YFE0117500)、国家自然科学基金(42406161, 42476160, 41776104)、上海市海洋局科研项目(HHK‐2023‐06)资助。
4 文献信息
Zhou, Z., Kuai, Y., Ge, J., van Maren, B., Wang, Z., Huang, K., et al. (2025). Modeling non-stationary wind-induced fluid motions with physics-informed neural networks for the shallow water equations in a polar coordinate system. Water Resources Research, 61, e2024WR037490. https://doi.org/10.1029/2024WR037490